【pythonで数値解析】連結タンクモデルを解いてみる |

研究の場において、数値解析(数値シミュレーション)は、データ解析や実験、フィールドワークなどと並んで、1研究手法になってきています。特に最近はpythonの充実した数値計算ライブラリによって、数値解析をしたことのない人でも比較的簡単に数値シミュレーションに触れることができるようになってきています

ということで、私も数値シミュレーションについてある程度は理解しておこうということで、今回は一番基本的な数値解析の問題である「連結タンクモデル」についてpythonで学習していこうと思います。

連結タンクモデルの原理

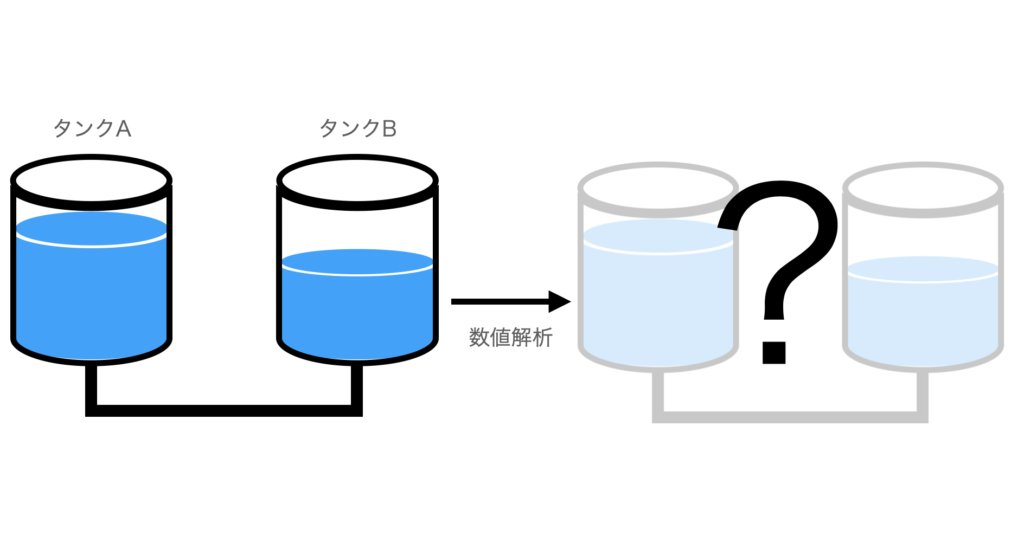
もっとも簡単な連結タンクの問題として、以下の画像のような2つの同じタンクが管でつながっているものを想定します。タンクAに水を多めに入れておき、タンクBには少なめに入れておいたとしましょう。

この時、管を通って水が移動できるとすると、タンクA, タンクBの水の水位はどのように変化するのか???

これを知るための手段として数値解析を使用します。
今回の問題では、別に数値解析を行わなくても、直感で水位の高いタンクAから水位の低いタンクBに水が移動し、最終的には両タンクの水位が同じになるという定性的なことは予想できます。

しかし、どのくらいの速さで水位が一定になるのか? 一定になる水位はいくつかなど定量的なことを知るためには数値解析が必要です。また、研究などをする場合においては、我々が知っている現象ばかりを扱うことはほとんどないので、数値解析を行い、直感的にわかりにくい現象をPC上で再現し調査します。このような意味から数値解析は数値シミュレーションなどとも呼ばれます。

(考え方)
まず初めは具体的な例から考えてみます。
上の状態をt=0(初期状態)とし、t=0〜1秒の間の両タンクの水位について考えます。
先ほど述べたように私たちは、定性的に水位の高いタンクAから水位の低いタンクBに水が流れることが予想できています。ではどのくらいの速さで水が移動するでしょうか?

ここで、満タンにたまったお風呂の水を栓を抜いて捨てる時を思い出してみてください。初めの方は勢い良く水が放出していき、水位も急激に低くなりますが、水位が低くなってくると水が放出する勢いは弱くなっていき水位の減少速度も小さくなりますよね。

つまり、タンクから水が出ていく速さは水位に依存していると考えられます。

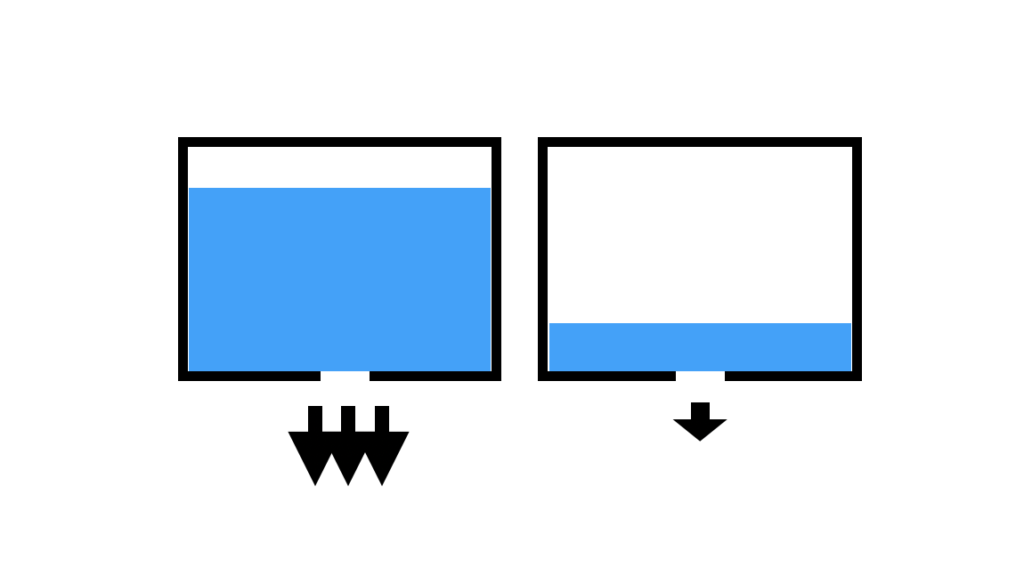
今回は水がタンクAからタンクBに流れる速さは、両タンクの水位差に比例するというふうにモデル化しましょう。式にすると次のようにかけます。

\(v = a(y_1-y_2)\)

\(v: 水の放出速度\\
a: 比例係数\\
y_1: タンクAの水位\\
y_2: タンクBの水位\)

t=0〜1の1秒間を考えると、タンクAからタンクBへ速さ\(v\)で水が流れることになります。
しかし、ここで問題があります。水が移動すると、水位が変化するので1秒後にタンクから水が出ていく速さは変化してしまうのです。このように刻一刻と変数が変化してしまう事象を反復的に解く時に数値解析の本領が発揮されます。

さて、今はt=0〜1の間だけを考えましたが、一般的に考えると今回の連結タンク問題は次のような式で書き表せます。

\(y_1(t+\Delta{t}) = y_1(t) – \frac{a(y_1(t)-y_2(t))\times\Delta{t}}{S_1}\)

\(y_2(t+\Delta{t}) = y_2(t) – \frac{a(y_1(t)-y_2(t))\times\Delta{t}}{S_2}\)

\(v: 水の放出速度 [m^3/s]\\
a: 比例係数\\
y_1: タンクAの水位 [m]\\
y_2: タンクBの水位 [m]\\
S_1: タンクAの底面の断面積 [m^2]\\
S_2: タンクBの底面の断面積 [m^2]\)

この式を用いて、以下pythonで数値計算をしてみましょう。

サンプルコード

サンプルコードは以下の通りになります。
このプログラムで設定している初期条件は以下の通りです。

初期条件

\(a = 0.2\\
y_1 = 18m\\
y_2 = 2m\\
\Delta{t} = 0.01\\
S_1 = 1 m^2\\
S_2 = 1 m^2\)


import numpy as np
import matplotlib.pyplot as plt

#パラメータの設定
S1 = pow(1,2)
S2 = pow(1,2)
y1 = 18
y2 = 2
DT = 0.01
T = 0
a = 0.2

#配列を用意
plotdata = np.array([[T, y1, y2]])

#main処理
for i in range(1600):
    y1 = plotdata[i, 1] - a*(plotdata[i, 1]-plotdata[i, 2])*(DT)/S1
    y2 = plotdata[i, 2] + a*(plotdata[i, 1]-plotdata[i, 2])*(DT)/S2
    plotdata = np.vstack([plotdata, np.array([(i+1)*DT, y1, y2])])
    
#draw
fig = plt.figure()
plt.xlabel("time[s]")
plt.ylabel("height[m]")
plt.plot(plotdata[:,0],plotdata[:,1])
plt.plot(plotdata[:,0],plotdata[:,2])
plt.grid(which='major',color='black',linestyle='dashed')
fig.savefig('test.jpg')
plt.show()

import numpy as np

import matplotlib.pyplot as plt

#パラメータの設定

S1 = pow(1,2)

S2 = pow(1,2)

y1 = 18

y2 = 2

DT = 0.01

T = 0

a = 0.2

#配列を用意

plotdata = np.array([[T, y1, y2]])

#main処理

for i in range(1600):

y1 = plotdata[i, 1] - a*(plotdata[i, 1]-plotdata[i, 2])*(DT)/S1

y2 = plotdata[i, 2] + a*(plotdata[i, 1]-plotdata[i, 2])*(DT)/S2

plotdata = np.vstack([plotdata, np.array([(i+1)*DT, y1, y2])])

#draw

fig = plt.figure()

plt.xlabel("time[s]")

plt.ylabel("height[m]")

plt.plot(plotdata[:,0],plotdata[:,1])

plt.plot(plotdata[:,0],plotdata[:,2])

plt.grid(which='major',color='black',linestyle='dashed')

fig.savefig('test.jpg')

plt.show()

結果

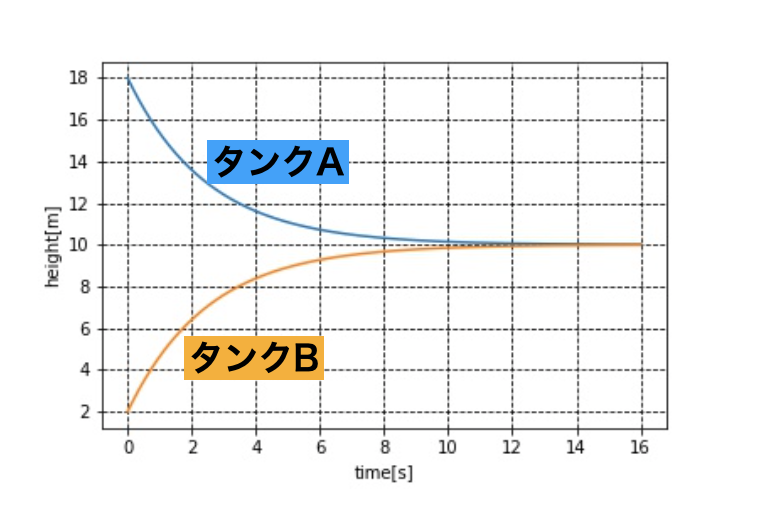
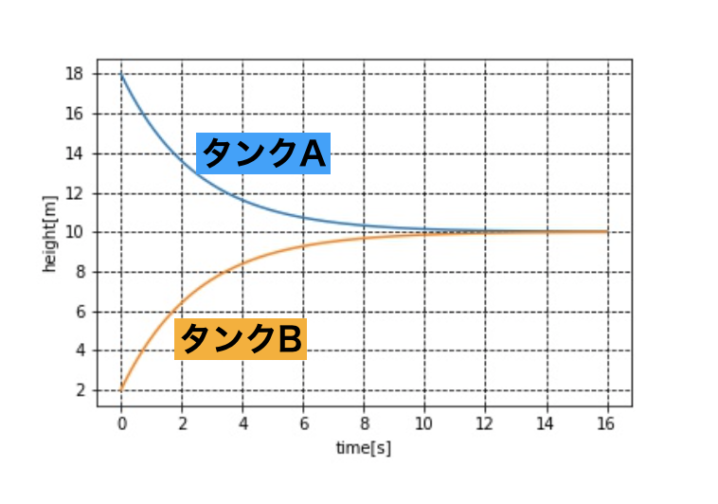
結果は以下のようになります。
約4秒後にはタンクAとタンクBの水位が一致し、その水位は10mになることがわかりました。

感想

とりあえずやってみた感想としては、「え? これが数値シミュレーション??」という感じですね笑
もっとアニメーションで動いたり、きれいに色がついていたりするグラフをよくみていたので、今回の結果だけではなんか期待外れな感じですね。

しかし、数値シミュレーションの本質は、解析解が得られない(解くのが難しい)方程式を近似的に解くことにあるので、今回の内容でも十分本質は理解できるかなと思います。もう少し勉強して2次元熱伝導方程式のアニメーションくらいは最低限できるように頑張ります。

参考書籍

数値解析のことを何も理解していない人におすすめの参考書がこれです。
従来の数値解析の参考書は最初から難しい数式が並んでいたり、理論から解説されているのですぐ眠くなってしまいますが、「マセマの数値解析」は理論はとりあえず置いておいて、プログラムを実際書いて例題を解くことで数値解析の面白さを理解させてくれるので、初学者の最初の一冊にうってつけです。